Demystifying The Karnaugh Map: A Powerful Tool For Boolean Simplification

Demystifying the Karnaugh Map: A Powerful Tool for Boolean Simplification

Related Articles: Demystifying the Karnaugh Map: A Powerful Tool for Boolean Simplification

Introduction

In this auspicious occasion, we are delighted to delve into the intriguing topic related to Demystifying the Karnaugh Map: A Powerful Tool for Boolean Simplification. Let’s weave interesting information and offer fresh perspectives to the readers.

Demystifying the Karnaugh Map: A Powerful Tool for Boolean Simplification

The realm of digital logic often involves intricate Boolean expressions that represent complex circuits. Simplifying these expressions is crucial for designing efficient and cost-effective circuits. One powerful tool that aids in this simplification process is the Karnaugh Map (K-map). This article delves into the intricacies of K-maps, outlining their significance and providing a comprehensive guide to their application.

The Essence of Karnaugh Maps

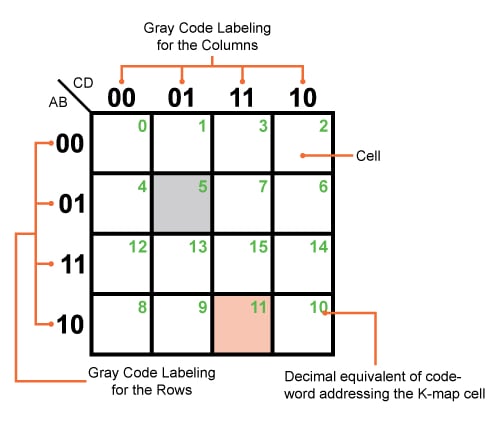
A Karnaugh map is a visual representation of a Boolean function, enabling the simplification of complex expressions through a systematic approach. It utilizes a grid format where each cell corresponds to a unique combination of input variables. These variables are typically binary, representing logic states of ‘0’ or ‘1’. The arrangement of cells within the grid follows a specific pattern, ensuring adjacent cells differ in only one variable, facilitating the identification of groups representing simplified terms.

Constructing the Karnaugh Map

The construction of a K-map involves the following steps:

1. Determine the Number of Input Variables: The number of input variables dictates the size of the K-map. A two-variable K-map requires a 2×2 grid, a three-variable K-map a 2×4 grid, and so on.

2. Label the Rows and Columns: Rows and columns are labeled with binary combinations representing the input variables. The labeling follows a Gray code pattern, where only one bit changes between adjacent rows or columns.

3. Populate the Cells: Each cell within the K-map corresponds to a unique combination of input variables. The value within each cell represents the output of the Boolean function for that specific input combination.

Simplifying Boolean Expressions with K-maps

The core principle behind K-map simplification lies in grouping adjacent cells containing ‘1’s. These groups represent simplified terms in the Boolean expression. The following rules guide the grouping process:

1. Adjacent Cells: Only cells that are adjacent horizontally, vertically, or diagonally can be grouped. This adjacency is determined by the Gray code labeling, ensuring only one variable differs between adjacent cells.

2. Group Size: The size of each group must be a power of two, representing a simplified term with a corresponding number of literals. For instance, a group of two cells represents a term with one literal, a group of four cells represents a term with two literals, and so on.

3. Largest Possible Groups: Aim to form the largest possible groups, encompassing as many ‘1’s as possible. This minimizes the number of terms in the simplified expression.

4. Overlapping Groups: Groups can overlap, with a single cell potentially being included in multiple groups. This is essential for maximizing the simplification process.

5. Essential Prime Implicants: Some groups are essential, meaning they encompass ‘1’s that cannot be covered by any other group. These essential prime implicants are crucial for the simplified expression.

Example: Simplifying a Three-Variable Function

Consider the Boolean function F(A, B, C) = Σ(0, 1, 2, 3, 4, 7). This expression represents the output of the function for specific combinations of input variables A, B, and C. To simplify this expression using a K-map, we follow these steps:

1. Construct the K-map: A three-variable K-map requires a 2×4 grid, with rows labeled with the combinations of variables A and B, and columns labeled with the combinations of variable C.

2. Populate the Cells: The cells corresponding to the minterms (0, 1, 2, 3, 4, 7) are marked with ‘1’s, and the remaining cells are marked with ‘0’s.

3. Form Groups: Two groups are formed: one group of four cells representing the term ‘A’ (covering minterms 0, 1, 4, 5), and another group of two cells representing the term ‘BC’ (covering minterms 2, 3).

4. Simplified Expression: The simplified expression for F(A, B, C) is therefore F(A, B, C) = A + BC.

Benefits of Using Karnaugh Maps

The use of Karnaugh maps offers several advantages in simplifying Boolean expressions:

1. Visual Approach: K-maps provide a visual representation of the Boolean function, allowing for intuitive understanding and simplification.

2. Systematic Method: The grouping rules ensure a systematic and organized approach to simplification, minimizing errors and ensuring optimal results.

3. Efficiency: K-maps streamline the simplification process, reducing the time and effort required compared to traditional algebraic methods.

4. Reduced Complexity: The simplified expressions obtained using K-maps are often significantly less complex than the original expressions, leading to simpler and more efficient circuits.

FAQs Regarding Karnaugh Maps

1. How do I handle "don’t care" conditions in a K-map?

"Don’t care" conditions represent input combinations where the output of the function is irrelevant. These conditions can be marked with an ‘X’ in the K-map. When grouping, "don’t care" conditions can be included in groups to form larger groups and simplify the expression further.

2. What are the limitations of K-maps?

While powerful, K-maps are limited in their application. For functions with a large number of variables (beyond five or six), the complexity of the map increases significantly, making it cumbersome to use.

3. Are there alternatives to K-maps for Boolean simplification?

Yes, other methods like the Quine-McCluskey algorithm and Boolean algebra manipulation can be used for simplification. However, K-maps offer a more intuitive and visual approach, making them particularly useful for beginners and for functions with a moderate number of variables.

Tips for Using Karnaugh Maps Effectively

1. Start with a Clear Understanding of Boolean Algebra: A strong foundation in Boolean algebra is essential for effectively applying K-maps.

2. Practice with Simple Examples: Begin with simple functions to understand the principles of grouping and simplification before tackling more complex examples.

3. Visualize the Adjacency: Pay close attention to the Gray code labeling and the concept of adjacency to ensure accurate grouping.

4. Maximize Group Size: Always aim to form the largest possible groups to minimize the number of terms in the simplified expression.

5. Check for Essential Prime Implicants: Identify essential prime implicants to ensure all ‘1’s are covered in the final expression.

Conclusion

The Karnaugh map provides a powerful and intuitive tool for simplifying Boolean expressions, leading to more efficient and cost-effective digital circuits. Its visual representation and systematic approach facilitate simplification, reducing complexity and enhancing design efficiency. While limitations exist for functions with a large number of variables, K-maps remain an invaluable tool for simplifying Boolean expressions, particularly for beginners and for functions with a moderate number of inputs. By mastering the principles of K-map construction and simplification, designers can effectively navigate the complex world of Boolean logic and create optimized digital circuits.

Closure

Thus, we hope this article has provided valuable insights into Demystifying the Karnaugh Map: A Powerful Tool for Boolean Simplification. We hope you find this article informative and beneficial. See you in our next article!