Demystifying The Power Of Karnaugh Maps: A Comprehensive Guide To Boolean Simplification

Demystifying the Power of Karnaugh Maps: A Comprehensive Guide to Boolean Simplification

Related Articles: Demystifying the Power of Karnaugh Maps: A Comprehensive Guide to Boolean Simplification

Introduction

In this auspicious occasion, we are delighted to delve into the intriguing topic related to Demystifying the Power of Karnaugh Maps: A Comprehensive Guide to Boolean Simplification. Let’s weave interesting information and offer fresh perspectives to the readers.

Demystifying the Power of Karnaugh Maps: A Comprehensive Guide to Boolean Simplification

In the realm of digital logic design, the ability to simplify complex Boolean expressions is paramount. This simplification not only enhances circuit efficiency but also reduces the number of logic gates required, leading to lower cost, improved performance, and reduced power consumption. Karnaugh Maps, often referred to as K-maps, provide a visual and intuitive method for achieving this simplification, offering a powerful alternative to algebraic manipulation.

Understanding the Foundation: Boolean Algebra and Logic Gates

Before delving into the intricacies of K-maps, it’s essential to grasp the fundamental concepts of Boolean algebra and logic gates. Boolean algebra, named after the mathematician George Boole, is a system of logic that deals with binary values – TRUE (1) and FALSE (0). Logic gates, the building blocks of digital circuits, perform specific logical operations on these binary inputs, producing a binary output.

Common logic gates include:

• AND gate: Outputs 1 only when all inputs are 1.
• OR gate: Outputs 1 when at least one input is 1.
• NOT gate: Inverts the input, outputting 1 when the input is 0 and vice versa.
• XOR gate: Outputs 1 when the inputs are different, and 0 when they are the same.

These gates, along with their corresponding Boolean expressions, form the basis for designing and analyzing digital circuits.

Introducing the Karnaugh Map: A Visual Approach to Boolean Simplification

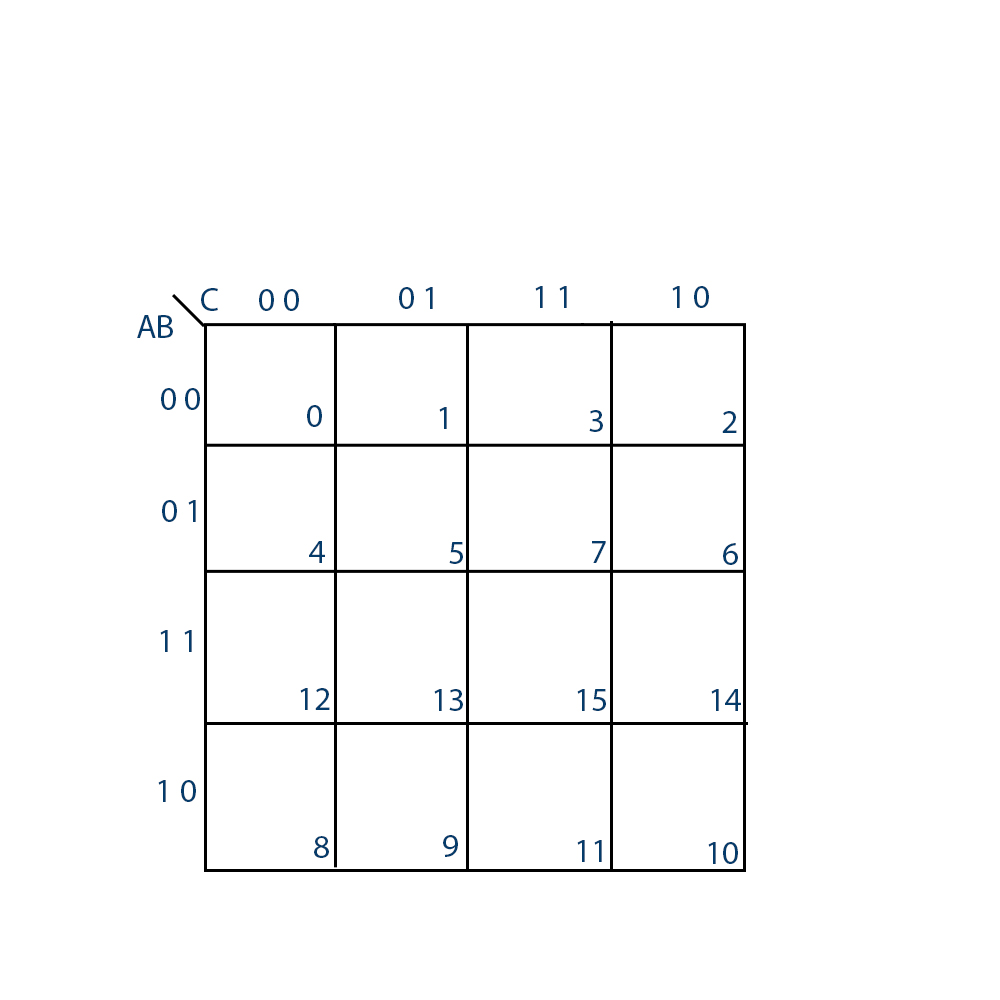
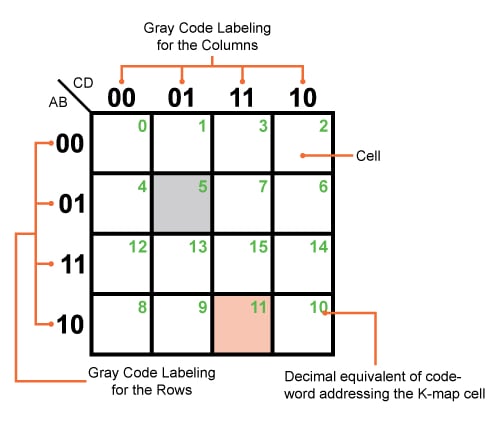
The Karnaugh Map (K-map) is a graphical representation of a Boolean function, offering a visual aid for simplification. It is a two-dimensional grid where each cell represents a unique combination of input variables. The arrangement of cells is crucial – adjacent cells differ by only one variable, ensuring that adjacent cells represent minterms (product terms) that differ by a single literal.

Construction of a Karnaugh Map

The construction of a K-map depends on the number of input variables. For a function with ‘n’ variables, the K-map will have 2^n cells. The rows and columns of the map are labeled with binary codes representing the input variables, ensuring that adjacent cells differ by only one bit.

Interpreting the K-map: Identifying Essential Prime Implicants

Once the K-map is constructed, the function’s truth table values (0 or 1) are entered into the corresponding cells. The goal is then to identify groups of adjacent 1s, called prime implicants. These groups represent simplified product terms that cover the original function.

A prime implicant is a group of 1s that cannot be further combined with other groups to form a larger group. It is essential to identify all prime implicants as they are the building blocks for simplifying the Boolean expression.

K-Map Rules: Guiding the Simplification Process

The simplification process involves identifying and combining prime implicants based on the following rules:

1. Group 1s: Group together adjacent 1s, forming rectangular or square shapes. These groups must have dimensions that are powers of two (1, 2, 4, 8, etc.).
2. Maximize Group Size: Prioritize larger groups over smaller groups, as they represent more simplified terms.
3. Include All 1s: Ensure all 1s on the map are covered by at least one group.
4. Minimize the Number of Groups: Use the fewest number of groups possible to cover all 1s.
5. Don’t Care Conditions: If a cell represents a "don’t care" condition (meaning its value can be either 0 or 1), it can be included in any group to potentially simplify the expression further.

Illustrative Example: Simplifying a Boolean Function Using a K-map

Let’s consider the Boolean function F(A, B, C) = Σm(0, 1, 2, 3, 5, 7), where Σm( ) represents the minterms of the function.

1. Construct the K-map: Create a 3-variable K-map with rows labeled with binary codes for variables A and B, and columns labeled with binary codes for variable C.

2. Populate the K-map: Enter 1s in the cells corresponding to the minterms listed in the function’s expression (0, 1, 2, 3, 5, 7).

3. Identify Prime Implicants: Group the 1s together, adhering to the K-map rules. In this example, we can identify two groups:

   • A group of four 1s, representing the term AB
   • A group of two 1s, representing the term C

4. Write the Simplified Expression: The simplified Boolean expression for the function is F(A, B, C) = AB + C.

Benefits of Using Karnaugh Maps

• Visual Simplification: K-maps provide a clear visual representation of the Boolean function, making it easier to identify and combine prime implicants.
• Intuitive Approach: The process of simplifying Boolean expressions using K-maps is intuitive and straightforward, even for beginners.
• Systematic Method: The rules of K-maps provide a structured and systematic approach to simplification, ensuring consistency and accuracy.
• Reduced Complexity: K-maps simplify complex Boolean expressions, reducing the number of logic gates required, leading to more efficient and cost-effective circuits.

FAQs about Karnaugh Maps

1. What is the maximum number of variables a K-map can handle effectively?

While K-maps can be constructed for functions with up to six variables, their effectiveness diminishes beyond four variables. For functions with more variables, other simplification methods like Quine-McCluskey algorithm become more practical.

2. Can K-maps be used for functions with "don’t care" conditions?

Yes, K-maps can effectively handle "don’t care" conditions. These conditions are represented by "X" in the map and can be included in any group to potentially simplify the expression further.

3. How do K-maps handle functions with multiple outputs?

For functions with multiple outputs, a separate K-map is constructed for each output. This allows for independent simplification of each output function.

4. What are the limitations of K-maps?

K-maps become less efficient and more complex as the number of variables increases. Additionally, they are not suitable for functions with a large number of minterms or complex logic expressions.

Tips for Using Karnaugh Maps Effectively

• Start with a Clear Truth Table: Ensure the truth table is accurately constructed before proceeding with the K-map.
• Label the Rows and Columns Carefully: Correct labeling of rows and columns is crucial for accurate mapping and simplification.
• Identify Prime Implicants Systematically: Use a systematic approach to identify all prime implicants, ensuring no group is missed.
• Don’t Forget the Don’t Cares: Utilize "don’t care" conditions to simplify the expression further.
• Double-Check Your Work: Verify the simplified expression against the original truth table to ensure accuracy.

Conclusion

Karnaugh maps offer a powerful and intuitive method for simplifying Boolean expressions, providing a visual and structured approach to the process. Their ability to reduce the complexity of logic circuits, enhance efficiency, and lower costs makes them an indispensable tool for digital logic designers. By mastering the rules of K-maps and applying them effectively, engineers can optimize circuit design and achieve optimal performance in their digital systems.

Closure

Thus, we hope this article has provided valuable insights into Demystifying the Power of Karnaugh Maps: A Comprehensive Guide to Boolean Simplification. We hope you find this article informative and beneficial. See you in our next article!