Demystifying The Power Of Karnaugh Maps And Their Applications

Demystifying the Power of Karnaugh Maps and Their Applications

Related Articles: Demystifying the Power of Karnaugh Maps and Their Applications

Introduction

In this auspicious occasion, we are delighted to delve into the intriguing topic related to Demystifying the Power of Karnaugh Maps and Their Applications. Let’s weave interesting information and offer fresh perspectives to the readers.

Demystifying the Power of Karnaugh Maps and Their Applications

The realm of digital logic design is intricately woven with the concept of Boolean algebra. This mathematical framework provides the foundation for representing and manipulating logical relationships, ultimately leading to the creation of complex digital circuits. While Boolean algebra offers a powerful tool, its direct application in simplifying complex expressions can be cumbersome. This is where Karnaugh Maps (K-maps) emerge as a visually intuitive and efficient method for simplifying Boolean expressions, streamlining the design process and leading to more optimized digital circuits.

Understanding Karnaugh Maps: A Visual Approach to Boolean Simplification

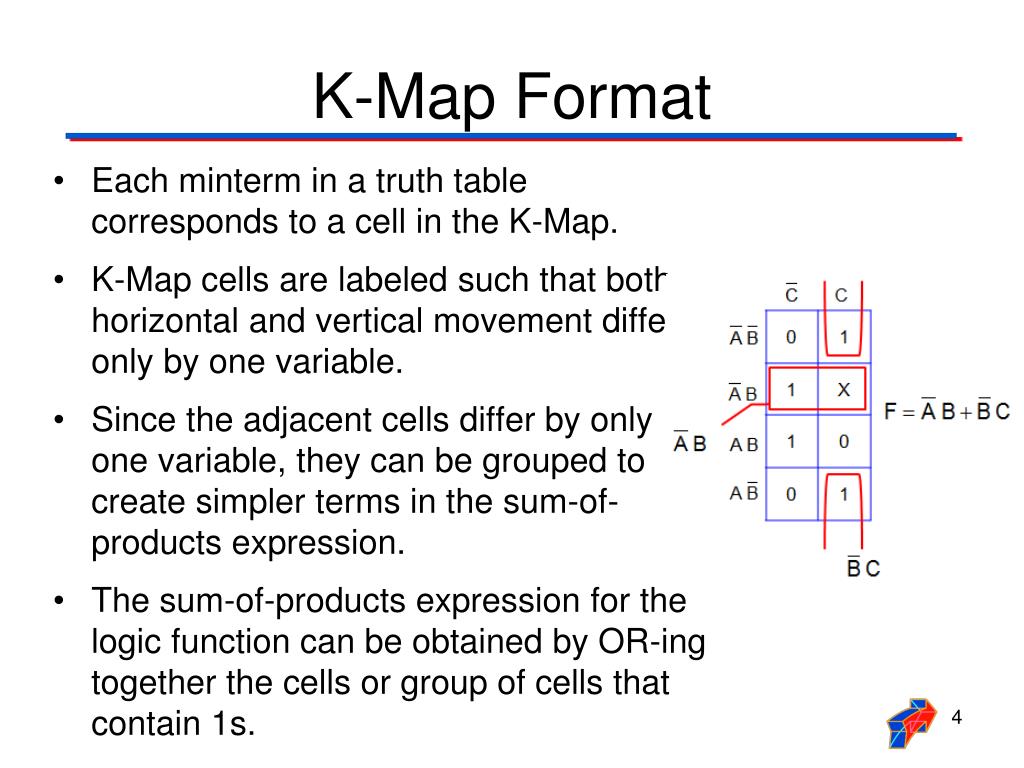
A Karnaugh map, often referred to as a K-map, is a graphical representation of a Boolean function. It provides a systematic way to visualize and manipulate Boolean expressions, making the simplification process significantly easier compared to traditional algebraic methods.

Key Components of a Karnaugh Map:

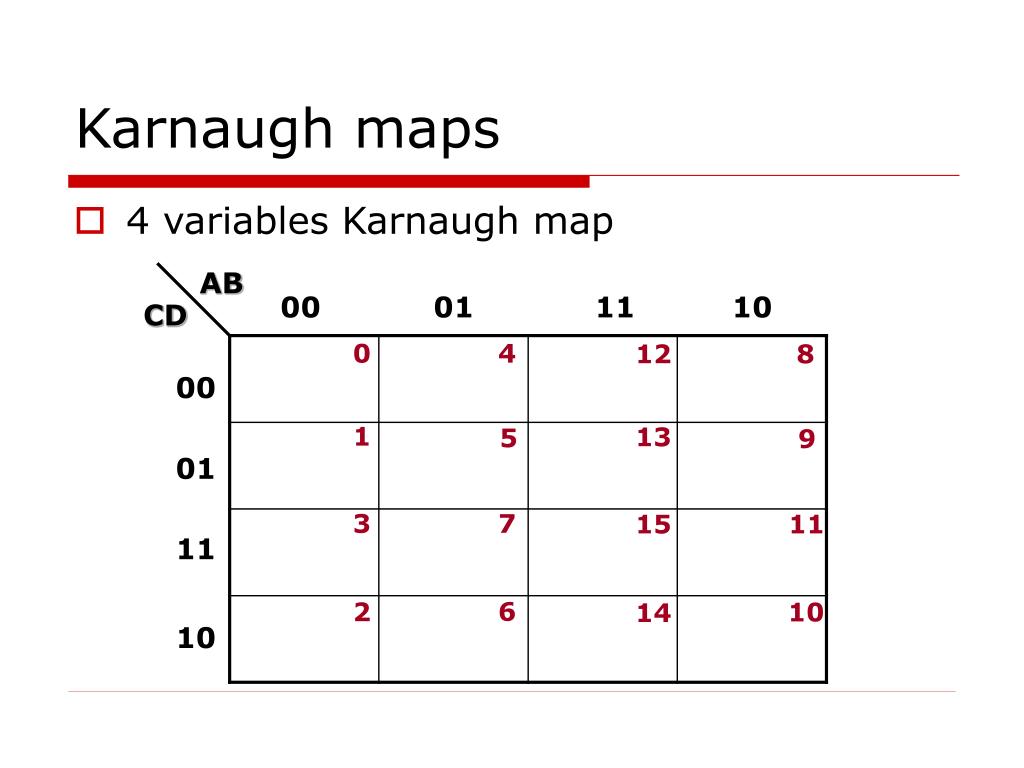
1. Cells: The map consists of a grid of cells, each representing a unique combination of input variables. The number of cells is determined by the number of input variables (2^n cells for n input variables).
2. Adjacent Cells: Cells that share a single variable changing are considered adjacent. This adjacency is crucial for identifying groups of minterms and maxterms, which form the basis for simplification.
3. Binary Representation: Each cell is labeled with a binary code representing the input variable combination. The labeling is done in a Gray code sequence, ensuring that adjacent cells differ by only one bit.
4. Minterms and Maxterms: A minterm is a product term that represents a single cell in the K-map. A maxterm, on the other hand, is a sum term that represents all cells except the one it corresponds to.

The Process of Simplification:

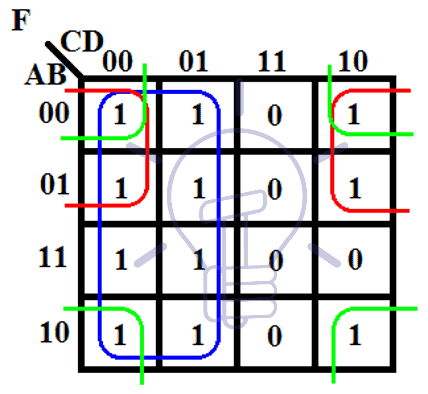
1. Mapping the Function: The first step involves representing the Boolean function on the K-map by placing a ‘1’ in the cells corresponding to the minterms of the function.
2. Grouping Adjacent Ones: Adjacent cells containing ‘1’s are grouped together. These groups represent simplified terms in the Boolean expression. The goal is to form the largest possible groups, ensuring that each ‘1’ is included in at least one group.
3. Identifying Simplified Terms: Each group corresponds to a simplified term. The simplified term is obtained by identifying the variables that remain constant within the group. If a variable changes its value within the group, it is excluded from the term.
4. Final Expression: The simplified Boolean expression is obtained by combining the simplified terms obtained from the grouped ‘1’s.

Advantages of Using Karnaugh Maps:

1. Visual Simplification: K-maps provide a visual representation of the Boolean function, making it easier to identify and group adjacent minterms.
2. Intuitive Approach: The graphical nature of K-maps makes the simplification process more intuitive, eliminating the need for complex algebraic manipulations.
3. Optimization: K-maps allow for the identification of minimal sum-of-products (SOP) or product-of-sums (POS) expressions, leading to optimized digital circuits with fewer logic gates.
4. Handling Multiple Variables: K-maps can effectively handle functions with up to four input variables. For functions with more variables, alternative methods like Quine-McCluskey algorithm are often employed.

Applications of Karnaugh Maps:

K-maps are widely used in various digital logic design applications, including:

1. Logic Circuit Minimization: Simplifying Boolean expressions leads to circuits with fewer logic gates, resulting in lower cost, reduced power consumption, and improved performance.
2. Digital System Design: K-maps are essential for designing digital systems, such as adders, subtractors, multiplexers, decoders, and other combinational logic circuits.
3. Troubleshooting and Debugging: K-maps help identify potential errors in digital circuits by providing a visual representation of the logic function and highlighting inconsistencies.
4. Education and Training: K-maps serve as a valuable teaching tool for introducing students to Boolean algebra and digital logic design concepts.

Beyond Simplification: The Power of K-maps in Design

While primarily known for their simplification capabilities, K-maps offer a deeper understanding of Boolean functions and their relationships. They provide a framework for analyzing and manipulating logical expressions, leading to insights that can be applied beyond circuit optimization.

K-maps can be used to:

1. Identify Essential Prime Implicants: These are simplified terms that are essential for covering all ‘1’s in the K-map.
2. Determine Don’t Care Conditions: In some cases, certain input combinations may not be relevant or feasible. K-maps allow for the inclusion of "don’t care" conditions, further simplifying the Boolean expression.
3. Analyze Complex Logic Functions: By representing the function on a K-map, it becomes easier to identify patterns and relationships between input variables, aiding in understanding the overall behavior of the logic function.

FAQs: Addressing Common Questions about Karnaugh Maps

1. What is the maximum number of variables a K-map can handle?

While K-maps can be used for functions with up to four variables, their effectiveness decreases for higher-order functions. For functions with more than four variables, alternative methods like the Quine-McCluskey algorithm are preferred.

2. Can K-maps handle functions with multiple outputs?

Yes, K-maps can be used for functions with multiple outputs. Separate K-maps are created for each output, and the simplification process is applied independently.

3. How do I handle "don’t care" conditions in a K-map?

"Don’t care" conditions are represented by an "X" in the K-map. These cells can be included in groups to further simplify the expression, as they can be assigned either a ‘0’ or a ‘1’ depending on what leads to the most simplified expression.

4. What are some common mistakes made when using K-maps?

Common mistakes include:

• Incorrectly grouping adjacent cells: Ensure that cells are grouped correctly, considering the Gray code sequence and adjacency rules.
• Missing essential prime implicants: Carefully identify all essential prime implicants to ensure the simplified expression covers all ‘1’s in the K-map.
• Incorrectly handling "don’t care" conditions: Ensure that "don’t care" conditions are used strategically to achieve maximum simplification.

Tips for Using Karnaugh Maps Effectively:

1. Start with a clear understanding of the Boolean function: Define the input variables and the desired output function before constructing the K-map.
2. Use the Gray code sequence for labeling cells: This ensures that adjacent cells differ by only one bit, simplifying the identification of adjacent groups.
3. Identify all essential prime implicants: Ensure that the simplified expression includes all essential prime implicants, which are necessary for covering all ‘1’s in the K-map.
4. Use "don’t care" conditions strategically: Include "don’t care" conditions to simplify the expression further, but ensure that they are used correctly.
5. Practice with various examples: Working through different examples will help you become more comfortable with the process and identify common patterns.

Conclusion: The Enduring Significance of Karnaugh Maps

Karnaugh maps remain a valuable tool in digital logic design, offering a visually intuitive and efficient method for simplifying Boolean expressions. Their ability to streamline the design process, optimize circuits, and provide a deeper understanding of logical relationships continues to make them a cornerstone of digital logic design. While advancements in automated tools have emerged, K-maps continue to play a crucial role in education, design, and troubleshooting, offering a fundamental understanding of Boolean functions and their applications in the world of digital circuits.

Closure

Thus, we hope this article has provided valuable insights into Demystifying the Power of Karnaugh Maps and Their Applications. We hope you find this article informative and beneficial. See you in our next article!