Unlocking Boolean Simplification: A Comprehensive Guide to Karnaugh Maps with 4 Variables
Related Articles: Unlocking Boolean Simplification: A Comprehensive Guide to Karnaugh Maps with 4 Variables
Introduction
With enthusiasm, let’s navigate through the intriguing topic related to Unlocking Boolean Simplification: A Comprehensive Guide to Karnaugh Maps with 4 Variables. Let’s weave interesting information and offer fresh perspectives to the readers.
Table of Content
Unlocking Boolean Simplification: A Comprehensive Guide to Karnaugh Maps with 4 Variables

The realm of digital logic thrives on the manipulation of Boolean expressions, which represent the intricate relationships between binary inputs and outputs. While these expressions can be complex, simplifying them is crucial for designing efficient and cost-effective digital circuits. Here, Karnaugh Maps (K-maps) emerge as a powerful tool, providing a visual and intuitive method for minimizing Boolean expressions, particularly for those involving up to four variables.
Understanding the Fundamentals
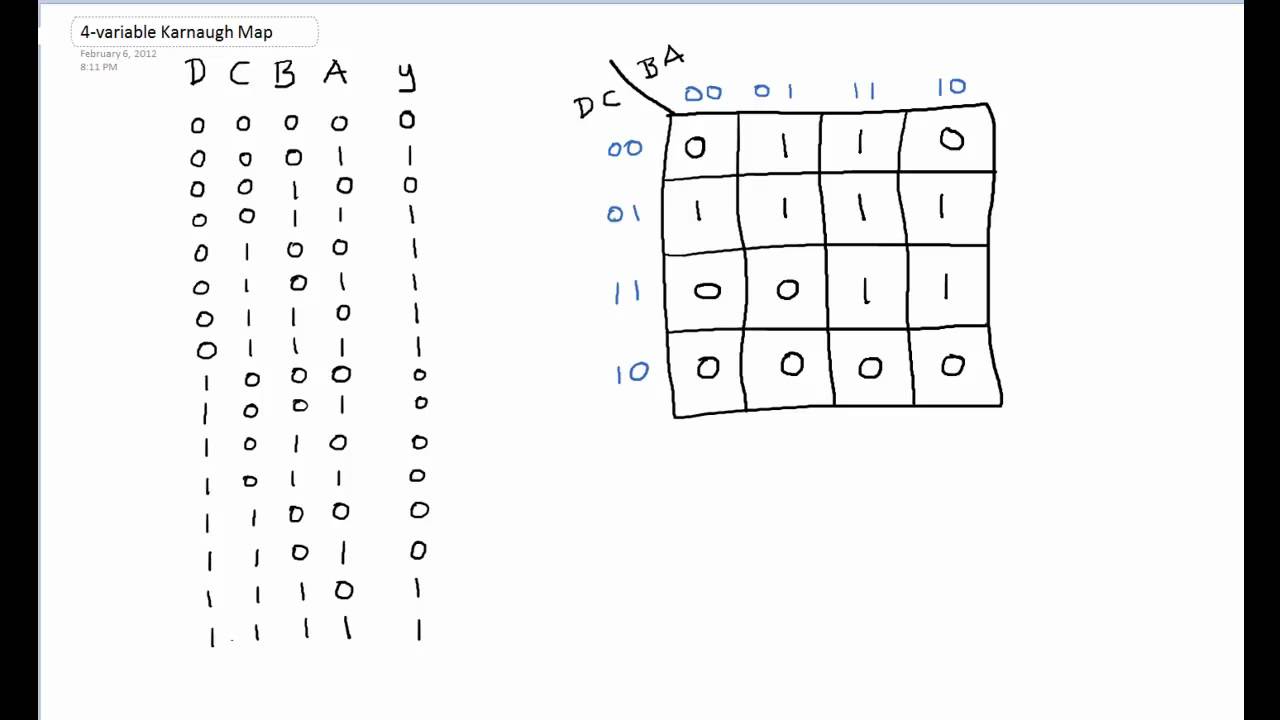
A K-map is a graphical representation of a truth table, where each cell corresponds to a unique combination of input variables. The arrangement of cells is not arbitrary; it follows a specific pattern based on the Gray code, ensuring that adjacent cells differ by only a single variable. This adjacency, even for seemingly distant cells on the map, is fundamental to K-map simplification.
For a 4-variable K-map, the arrangement typically follows a 2×4 grid, with rows representing one pair of variables and columns representing the other. Each cell is labeled with the corresponding minterm, a product term representing a unique combination of input variables.
The Art of Grouping: Identifying Essential Prime Implicants
The core of K-map simplification lies in grouping adjacent cells containing ‘1’s, representing minterms that can be combined. The groups must be rectangular or square, with dimensions that are powers of two (1, 2, 4, 8, etc.). These groups represent simplified product terms, known as prime implicants, which cover the original minterms.
Key Rules for Effective Grouping:
- Maximize Group Size: Aim to create the largest possible groups, encompassing as many ‘1’s as possible. This reduces the number of product terms in the simplified expression.
- Adjacent Cells: Groups can be formed by combining cells that are physically adjacent or considered adjacent due to the wrapping nature of the K-map. This means that cells on the extreme ends of a row or column are considered adjacent.
- No Isolated ‘1’s: Every ‘1’ on the map must be included in at least one group.
- Essential Prime Implicants: A prime implicant is considered essential if it covers a ‘1’ that cannot be covered by any other prime implicant. These essential prime implicants must be included in the simplified expression.
Illustrative Example: Simplifying a Boolean Expression
Let’s consider a Boolean expression with four variables: A, B, C, and D, represented by the following truth table:
| A | B | C | D | Output |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 1 |
| 0 | 0 | 0 | 1 | 1 |
| 0 | 0 | 1 | 0 | 0 |
| 0 | 0 | 1 | 1 | 1 |
| 0 | 1 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 | 1 |
| 0 | 1 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 0 |
| 1 | 0 | 1 | 1 | 0 |
| 1 | 1 | 0 | 0 | 0 |
| 1 | 1 | 0 | 1 | 0 |
| 1 | 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 | 0 |
This truth table can be represented by the following Boolean expression:
Output = A'B'C'D' + A'B'C'D + A'B'CD + A'BC'D + A'BCD To simplify this expression, we can utilize a K-map. The K-map for this expression would look like this:
| CD | 00 | 01 | 11 | 10 |
|---|---|---|---|---|
| AB | ||||
| 00 | 1 | 1 | 1 | 0 |
| 01 | 0 | 1 | 1 | 0 |
| 11 | 0 | 0 | 0 | 0 |
| 10 | 0 | 0 | 0 | 0 |
We can form the following groups:
- Group 1: Encompasses the four ‘1’s in the top row. This group represents the simplified product term A’B’.
- Group 2: Covers the two ‘1’s in the second row. This group represents the simplified product term A’CD.
Therefore, the simplified Boolean expression becomes:
Output = A'B' + A'CDThis simplified expression is equivalent to the original expression but is significantly easier to implement in a digital circuit.
Advantages of Using K-Maps
- Visual Simplification: K-maps provide a visual representation of Boolean expressions, making it easier to identify and combine minterms.
- Intuitive Process: The grouping process is intuitive and straightforward, even for beginners.
- Reduced Complexity: K-maps effectively simplify complex expressions, leading to more efficient and cost-effective circuit designs.
- Systematic Approach: The process of grouping and identifying prime implicants is systematic and well-defined, ensuring consistent results.
FAQs
Q: What are the limitations of K-maps?
A: While effective for up to four variables, K-maps become cumbersome and less practical for expressions with five or more variables.
Q: How do I handle ‘don’t care’ conditions in a K-map?
A: ‘Don’t care’ conditions, represented by ‘X’ in the truth table, can be included in groups to further simplify the expression. However, they are not mandatory for forming groups.
Q: Can K-maps be used for both sum-of-products (SOP) and product-of-sums (POS) forms?
A: Yes, K-maps can be used for both forms. For POS, you would group the ‘0’s instead of the ‘1’s.
Tips for Using K-Maps Effectively
- Practice Makes Perfect: Familiarize yourself with the K-map structure and grouping rules through practice exercises.
- Start with the Truth Table: Always begin with a clear and accurate truth table representing the Boolean expression.
- Identify Essential Prime Implicants: Prioritize identifying and including essential prime implicants in your simplified expression.
- Consider ‘Don’t Care’ Conditions: Explore the possibility of including ‘don’t care’ conditions to further optimize the expression.
Conclusion
Karnaugh maps serve as a powerful tool for simplifying Boolean expressions, offering a visual and intuitive approach to minimizing logic circuits. Their effectiveness lies in their ability to represent truth tables graphically, facilitating the identification and combination of minterms. Mastering K-map techniques empowers engineers and designers to create efficient and cost-effective digital systems, paving the way for innovative and complex designs.






Closure
Thus, we hope this article has provided valuable insights into Unlocking Boolean Simplification: A Comprehensive Guide to Karnaugh Maps with 4 Variables. We appreciate your attention to our article. See you in our next article!
