Unlocking The Power Of Logic: A Comprehensive Guide To Karnaugh Maps And Their Applications

Unlocking the Power of Logic: A Comprehensive Guide to Karnaugh Maps and Their Applications

Related Articles: Unlocking the Power of Logic: A Comprehensive Guide to Karnaugh Maps and Their Applications

Introduction

With enthusiasm, let’s navigate through the intriguing topic related to Unlocking the Power of Logic: A Comprehensive Guide to Karnaugh Maps and Their Applications. Let’s weave interesting information and offer fresh perspectives to the readers.

Unlocking the Power of Logic: A Comprehensive Guide to Karnaugh Maps and Their Applications

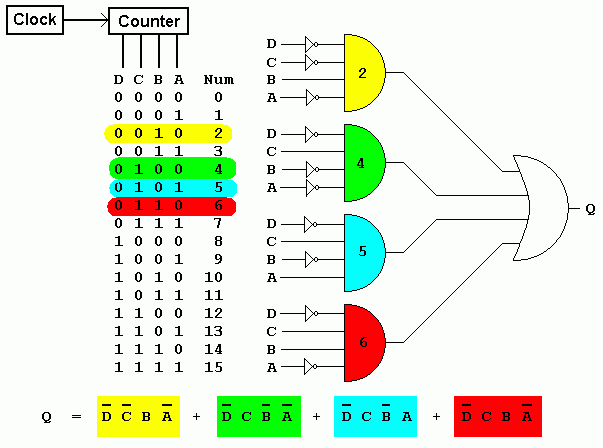
The realm of digital logic design is built upon a foundation of Boolean algebra, a system of mathematics that deals with logical operations. One of the fundamental challenges in this field is simplifying complex Boolean expressions, a task that is crucial for creating efficient and cost-effective digital circuits. Enter the Karnaugh map, a visual tool that offers a systematic and intuitive approach to Boolean simplification, making it a cornerstone in the world of digital circuit design.

Understanding the Essence of Karnaugh Maps

A Karnaugh map, often referred to as a K-map, is a graphical representation of a truth table, a tabular format that displays the output of a Boolean function for all possible combinations of its input variables. The K-map’s unique structure, based on a grid arrangement, allows for the identification of adjacent cells with common logical terms, leading to the simplification of the Boolean expression.

Visualizing Logic: The Structure of a K-map

The K-map’s grid consists of cells, each representing a unique combination of input variables. The number of cells in a K-map is determined by the number of input variables (n) and is equal to 2^n. The rows and columns of the K-map are labeled with binary codes, ensuring that adjacent cells differ by only one bit. This arrangement facilitates the identification of groups of adjacent cells that share common logical terms.

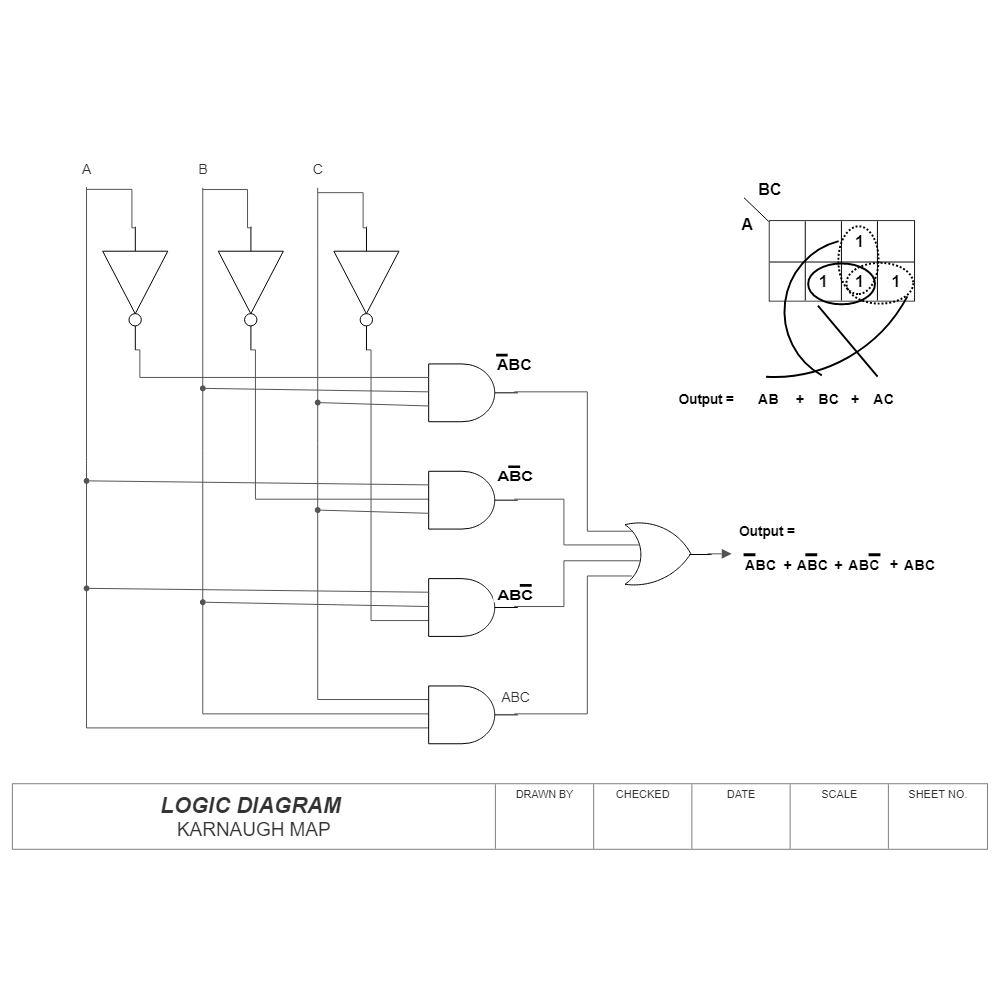
Simplifying Expressions: The Art of Grouping

The core principle of K-map simplification lies in identifying groups of adjacent cells containing "1" entries, representing "true" outputs. These groups are called "adjacencies," and they must adhere to specific rules:

• Adjacency: Cells are considered adjacent if they share a common side, even if they are located at opposite ends of a row or column.
• Group Size: Groups must be powers of two (1, 2, 4, 8, etc.) and should be as large as possible.
• Maximum Coverage: Each "1" entry must be included in at least one group, and no "0" entry should be included in any group.

From Groups to Expressions: Deriving the Simplified Logic

Once the adjacencies are identified, the simplified Boolean expression is derived by identifying the common variables within each group. A variable is considered "common" if it remains constant within the group. The resulting terms are then combined using the OR operator, representing the union of all the groups.

Beyond Simplification: Applications of K-maps

The power of K-maps extends far beyond simply simplifying Boolean expressions. They find applications in various aspects of digital logic design, including:

• Circuit Minimization: K-maps help reduce the number of logic gates required to implement a function, leading to smaller, more efficient circuits.
• Logic Function Design: K-maps are used to design and implement complex logic functions by directly mapping the desired output behavior to the K-map grid.
• Fault Detection: By analyzing the K-map, potential faults in a circuit can be identified and addressed, enhancing reliability.
• Truth Table Generation: K-maps can be used to generate truth tables from a given Boolean expression or circuit design.

Frequently Asked Questions (FAQs) About Karnaugh Maps

1. What are the advantages of using K-maps for Boolean simplification?

K-maps provide a visual and intuitive approach to simplification, making it easier to grasp the relationships between input variables and output values. Their graphical nature reduces the complexity associated with algebraic manipulation, especially for functions with a large number of variables.

2. Are there any limitations to using K-maps?

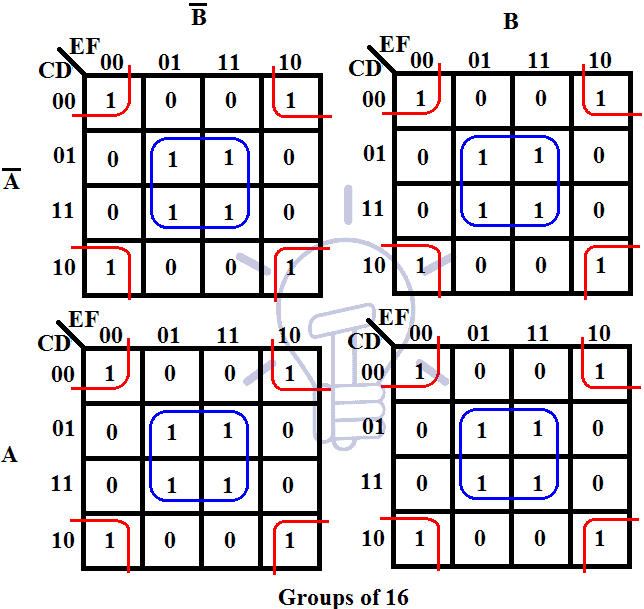
While K-maps are effective for simplifying functions with up to six variables, their practicality diminishes for functions with more variables due to the increasing size and complexity of the map. Additionally, K-maps may not be suitable for certain types of functions, such as those with multiple outputs or complex logic.

3. How do I choose the right K-map for a given function?

The size of the K-map is determined by the number of input variables. A K-map with n input variables will have 2^n cells. Therefore, you need to choose a K-map that matches the number of input variables in your function.

4. How can I learn to use K-maps effectively?

Practice is key. Start by working through simple examples with a small number of variables and gradually increase the complexity. There are numerous resources available, including textbooks, online tutorials, and interactive tools, that can guide you through the process.

5. What are some common mistakes to avoid when using K-maps?

• Incorrect Adjacency: Ensuring that groups are formed correctly, respecting the rules of adjacency and group size.
• Incomplete Coverage: Making sure that all "1" entries are included in at least one group.
• Incorrect Term Derivation: Accurately identifying the common variables within each group and combining them correctly.

Tips for Mastering Karnaugh Maps

• Start Simple: Begin with small functions and gradually increase the complexity.
• Visualize the Adjacency: Use colored pencils or highlighters to identify groups and visualize the connections between cells.
• Check for Completeness: Ensure that all "1" entries are covered by at least one group.
• Simplify Step-by-Step: Break down the simplification process into smaller steps, focusing on one group at a time.
• Review and Verify: Double-check your work to ensure accuracy and completeness.

Conclusion: Empowering Digital Design with K-maps

Karnaugh maps stand as a powerful tool in the digital logic designer’s arsenal, offering a visual and intuitive approach to simplifying Boolean expressions. By understanding the structure, rules, and applications of K-maps, engineers can design and implement efficient and reliable digital circuits, paving the way for advancements in computing and electronics. Their ability to translate complex logic into a simplified form, while ensuring optimal circuit performance, makes them an indispensable tool for anyone working in the field of digital design.

Closure

Thus, we hope this article has provided valuable insights into Unlocking the Power of Logic: A Comprehensive Guide to Karnaugh Maps and Their Applications. We hope you find this article informative and beneficial. See you in our next article!