Unraveling The Essence Of UMAP: A Comprehensive Guide To Understanding Its Significance

Unraveling the Essence of UMAP: A Comprehensive Guide to Understanding Its Significance

Related Articles: Unraveling the Essence of UMAP: A Comprehensive Guide to Understanding Its Significance

Introduction

With great pleasure, we will explore the intriguing topic related to Unraveling the Essence of UMAP: A Comprehensive Guide to Understanding Its Significance. Let’s weave interesting information and offer fresh perspectives to the readers.

Unraveling the Essence of UMAP: A Comprehensive Guide to Understanding Its Significance

The landscape of data analysis is constantly evolving, driven by the ever-increasing volume and complexity of data. Amidst this evolution, dimensionality reduction techniques have emerged as powerful tools for navigating the intricacies of high-dimensional datasets. One such technique, gaining significant traction in the realm of data exploration and visualization, is Uniform Manifold Approximation and Projection (UMAP). This article aims to provide a comprehensive understanding of UMAP, delving into its core principles, applications, and significance in the context of modern data analysis.

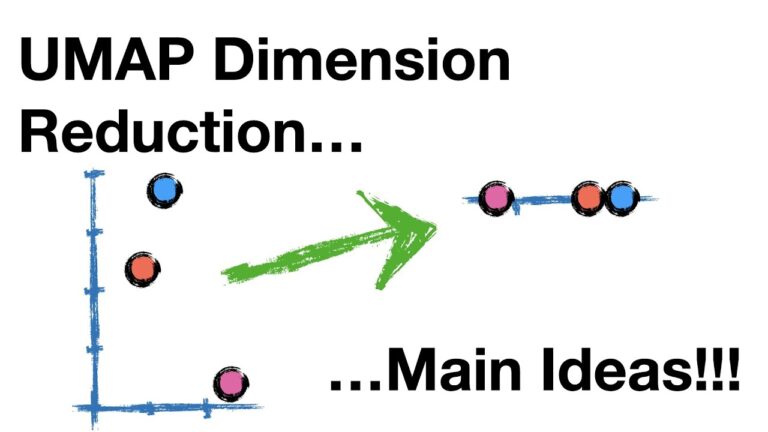
Understanding the Essence of UMAP

At its heart, UMAP seeks to find a lower-dimensional representation of high-dimensional data while preserving the underlying structure and relationships within the data. This process involves two key steps:

1. Finding the Manifold: UMAP assumes that the data points reside on a low-dimensional manifold embedded within a higher-dimensional space. It strives to identify this manifold, essentially the "true" structure of the data, by constructing a neighborhood graph that captures local relationships between data points.

2. Projection: Once the manifold is identified, UMAP projects the data points onto this lower-dimensional space, preserving the local neighborhood structure and global relationships as much as possible. This projection results in a visually interpretable representation of the data, facilitating insights that might be obscured in the original high-dimensional space.

The Advantages of UMAP

UMAP offers several advantages over traditional dimensionality reduction techniques, making it a valuable tool for a wide range of applications:

• Preservation of Global Structure: Unlike techniques like Principal Component Analysis (PCA), which focus primarily on capturing variance, UMAP excels at preserving the global structure of the data. This ensures that the projected representation accurately reflects the relationships between different clusters or groups within the dataset.

• Robustness to Noise: UMAP is robust to noise and outliers, which can significantly distort the results of other dimensionality reduction techniques. This robustness stems from its reliance on local neighborhood information, making it less susceptible to the influence of individual outliers.

• Scalability: UMAP is designed to handle large datasets efficiently. Its computational complexity scales well with the number of data points, making it practical for analyzing massive datasets.

• Intuitive Visualization: The projected representation generated by UMAP is often visually intuitive, enabling researchers to quickly grasp the underlying structure of the data and identify interesting patterns or anomalies.

Applications of UMAP

The versatility of UMAP makes it suitable for a wide range of applications across diverse domains:

• Data Exploration and Visualization: UMAP is a powerful tool for exploring and visualizing complex datasets, revealing hidden patterns and relationships that might not be apparent in the original high-dimensional space.

• Clustering and Classification: UMAP can be used to enhance clustering and classification algorithms by providing a more informative representation of the data, leading to improved accuracy and interpretability.

• Anomaly Detection: By preserving the global structure of the data, UMAP can help identify outliers and anomalies that deviate significantly from the expected patterns.

• Machine Learning: UMAP can be used as a pre-processing step for machine learning models, reducing dimensionality and improving model performance by providing a more concise and informative representation of the data.

• Bioinformatics: UMAP has been successfully applied in bioinformatics for analyzing gene expression data, identifying cell types, and understanding the dynamics of biological systems.

• Image Analysis: UMAP can be used to analyze and visualize high-dimensional image data, enabling the identification of patterns and relationships between different image features.

• Natural Language Processing (NLP): UMAP can be applied to reduce the dimensionality of text data, facilitating the analysis and visualization of text corpora and the identification of semantic relationships between words and documents.

Understanding the UMAP Score

While UMAP itself doesn’t produce a specific "score," the process of applying UMAP generates a new representation of the data in a lower-dimensional space. This representation can then be further analyzed and interpreted using various metrics and techniques. The effectiveness of UMAP can be evaluated based on how well it preserves the structure and relationships of the original data in the lower-dimensional projection.

Frequently Asked Questions (FAQs) about UMAP

Q: What are the key parameters in UMAP and how do they affect the results?

A: UMAP utilizes several key parameters, including:

• Number of Neighbors: This parameter controls the size of the local neighborhood used for constructing the neighborhood graph. A higher number of neighbors leads to a more global view of the data, while a lower number focuses on local relationships.

• Minimum Distance: This parameter controls the degree of separation between data points in the lower-dimensional space. A higher minimum distance results in a more dispersed representation, while a lower value leads to a denser projection.

• Metric: UMAP allows for the selection of a distance metric, which determines how distances between data points are measured. Different metrics can lead to different representations, depending on the nature of the data.

Q: How can I choose the optimal parameters for my specific dataset?

A: Choosing the optimal parameters for UMAP requires a balance between preserving the underlying structure of the data and achieving a visually interpretable representation. Experimentation and visualization are key. Start with default values and adjust the parameters based on the specific characteristics of the data and the desired outcome.

Q: Can UMAP be used for both numerical and categorical data?

A: While UMAP is primarily designed for numerical data, it can also be applied to categorical data by encoding categorical variables into numerical representations. This can be achieved using techniques like one-hot encoding or ordinal encoding.

Q: How does UMAP compare to other dimensionality reduction techniques like PCA?

A: UMAP differs from PCA in several key aspects:

• Global Structure Preservation: UMAP focuses on preserving the global structure of the data, while PCA primarily captures variance.

• Nonlinear Relationships: UMAP can capture nonlinear relationships between data points, while PCA is limited to linear relationships.

• Robustness to Noise: UMAP is more robust to noise and outliers compared to PCA.

Tips for Effective UMAP Application

• Data Preprocessing: Ensure that the data is properly preprocessed before applying UMAP. This includes handling missing values, scaling numerical features, and encoding categorical variables appropriately.

• Experimentation: Experiment with different parameter settings to find the optimal configuration for your specific dataset and analysis objective.

• Visualization: Visualize the projected representation to gain insights into the underlying structure of the data and identify interesting patterns or anomalies.

• Combination with Other Techniques: UMAP can be effectively combined with other data analysis techniques, such as clustering, classification, and machine learning algorithms, to enhance their performance and interpretability.

Conclusion

UMAP stands as a powerful and versatile dimensionality reduction technique, offering numerous advantages over traditional methods. Its ability to preserve global structure, handle large datasets, and generate visually intuitive representations makes it an invaluable tool for exploring, visualizing, and analyzing complex data. By leveraging its unique capabilities, researchers and analysts can gain deeper insights into the underlying structure of their data, leading to more informed decisions and impactful discoveries. As the volume and complexity of data continue to grow, UMAP will undoubtedly play an increasingly significant role in shaping the future of data analysis.

Closure

Thus, we hope this article has provided valuable insights into Unraveling the Essence of UMAP: A Comprehensive Guide to Understanding Its Significance. We thank you for taking the time to read this article. See you in our next article!