Unveiling Hidden Structures: A Comprehensive Guide to Unsupervised Dimensionality Reduction with UMAP

Introduction

In this auspicious occasion, we are delighted to delve into the intriguing topic related to Unveiling Hidden Structures: A Comprehensive Guide to Unsupervised Dimensionality Reduction with UMAP. Let’s weave interesting information and offer fresh perspectives to the readers.

Unveiling Hidden Structures: A Comprehensive Guide to Unsupervised Dimensionality Reduction with UMAP

UMAP: An alternative dimensionality reduction technique by Fernando Luna MCD-UNISON Medium

The world of data is vast and often complex. As we gather more data, the challenge of understanding and extracting meaningful insights becomes increasingly difficult. This is where dimensionality reduction techniques come into play, offering a powerful tool for simplifying data by reducing the number of features or variables while preserving essential information. Among these techniques, Uniform Manifold Approximation and Projection (UMAP) stands out as a robust and versatile approach for unsupervised dimensionality reduction.

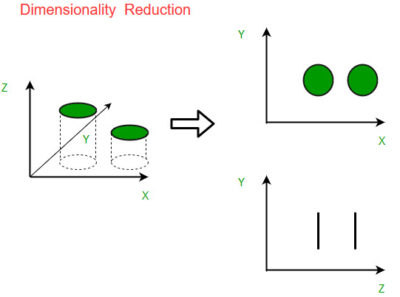
Understanding the Need for Dimensionality Reduction

Imagine trying to navigate a dense forest with countless trees. It would be overwhelming to consider every single tree individually. Instead, we might focus on identifying key landmarks, such as prominent hills or rivers, to simplify our understanding of the terrain. Similarly, in data analysis, we often face datasets with numerous features, making it challenging to discern patterns and relationships. Dimensionality reduction techniques provide a way to "map" our data onto a lower-dimensional space, highlighting the most relevant features and simplifying our analysis.

The Power of Unsupervised Learning

Traditional dimensionality reduction techniques, such as Principal Component Analysis (PCA), rely on supervised learning, requiring labeled data to identify the most significant features. However, in many real-world scenarios, labeled data is scarce or unavailable. This is where unsupervised learning methods like UMAP shine. UMAP excels at uncovering hidden structures and patterns within unlabeled data, making it invaluable for exploring and understanding complex datasets.

UMAP: A Geometric Approach to Dimensionality Reduction

UMAP’s strength lies in its ability to capture the underlying geometric structure of data. It assumes that data points are embedded in a manifold, a continuous, smooth surface that represents the true relationships between data points. UMAP then seeks to preserve these relationships by projecting the data onto a lower-dimensional space, ensuring that nearby points in the original space remain close in the reduced space.

Key Features of UMAP

  • Topological Data Analysis: UMAP leverages topological data analysis, a branch of mathematics that studies the shape and structure of data. This allows UMAP to capture complex relationships and identify non-linear patterns in the data.
  • Local Neighborhood Preservation: UMAP focuses on preserving local neighborhoods in the data, ensuring that nearby points in the high-dimensional space remain close in the low-dimensional representation.
  • Global Structure Preservation: While prioritizing local neighborhoods, UMAP also considers the global structure of the data, ensuring that distant points are also appropriately represented in the reduced space.
  • Speed and Efficiency: UMAP is known for its computational efficiency, making it suitable for analyzing large datasets.

Applications of UMAP

UMAP’s versatility makes it applicable across various domains:

  • Data Visualization: UMAP excels at visualizing high-dimensional data, enabling researchers to identify clusters, outliers, and other interesting patterns.
  • Clustering and Anomaly Detection: UMAP can be used to identify natural clusters within data, aiding in tasks like customer segmentation or anomaly detection.
  • Machine Learning: UMAP can be used as a preprocessing step for machine learning models, improving their performance by reducing dimensionality and simplifying the learning process.
  • Bioinformatics: UMAP is widely used in bioinformatics to analyze gene expression data, identify cell types, and study disease progression.

FAQs about UMAP

Q: What are the advantages of using UMAP compared to other dimensionality reduction techniques?

A: UMAP offers several advantages over traditional methods like PCA:

  • Non-linearity: UMAP can capture non-linear relationships in data, while PCA is limited to linear relationships.
  • Local Neighborhood Preservation: UMAP prioritizes preserving local neighborhoods, which is crucial for capturing fine-grained structures in the data.
  • Scalability: UMAP is designed to handle large datasets efficiently, making it suitable for real-world applications.

Q: How can I choose the optimal number of dimensions for UMAP?

A: There is no single best approach for selecting the optimal number of dimensions. Several methods can be employed:

  • Visual Inspection: Visualizing the projected data for different dimensions can help identify the point where the data becomes too compressed or loses significant information.
  • Silhouette Score: The silhouette score measures the similarity between data points within a cluster compared to points in other clusters. A higher silhouette score indicates better clustering and separation.
  • Cross-Validation: Using cross-validation to evaluate the performance of a downstream machine learning model with different numbers of dimensions can help determine the optimal value.

Q: What are some tips for using UMAP effectively?

A:

  • Data Preprocessing: Ensure that your data is properly preprocessed before applying UMAP. This may involve scaling, normalization, or handling missing values.
  • Parameter Tuning: Experiment with different UMAP parameters, such as the number of neighbors, the minimum distance, and the metric used to measure distances between data points.
  • Visual Inspection: Visualize the projected data to assess the quality of the reduction and identify any potential issues.
  • Compare with Other Methods: Consider comparing UMAP with other dimensionality reduction techniques to determine the most suitable method for your specific data and task.

Conclusion

UMAP represents a significant advancement in unsupervised dimensionality reduction, offering a powerful tool for exploring and understanding complex data. Its ability to capture non-linear relationships, preserve local neighborhoods, and maintain global structure makes it a valuable asset for researchers and practitioners across various fields. By leveraging UMAP’s capabilities, we can gain deeper insights into our data, uncover hidden patterns, and make more informed decisions. As data continues to grow exponentially, UMAP will undoubtedly play a critical role in shaping our understanding of the world around us.

UMAP based on the SOAP average similarity kernel Unsupervised Download Scientific Diagram UMAP Dimensionality Reduction - An Incredibly Robust Machine Learning Algorithm by Saul Dimensionality Reduction : PCA, tSNE, UMAP - Auriga IT
Uniform Manifold Approximation and Projection for Dimension Reduction Download Scientific UMAP Python: A Comprehensive Guide To Dimension Reduction Flowchart of the proposed SPCRGE for unsupervised dimensionality Download Scientific Diagram
Dimensionality reduction and unsupervised clustering of alignment Download Scientific Diagram Figure 1 from Unsupervised Dimensionality Reduction for Hyperspectral Imagery via Local

Closure

Thus, we hope this article has provided valuable insights into Unveiling Hidden Structures: A Comprehensive Guide to Unsupervised Dimensionality Reduction with UMAP. We hope you find this article informative and beneficial. See you in our next article!