Unveiling the Power of Dimensionality Reduction: A Comprehensive Look at UMAP

Introduction

With enthusiasm, let’s navigate through the intriguing topic related to Unveiling the Power of Dimensionality Reduction: A Comprehensive Look at UMAP. Let’s weave interesting information and offer fresh perspectives to the readers.

Unveiling the Power of Dimensionality Reduction: A Comprehensive Look at UMAP

Umap dimensionality reduction. (A) Cell distribution map of four tissue Download Scientific

Introduction

In the realm of data analysis, navigating complex, high-dimensional datasets can pose significant challenges. Visualizing patterns and extracting meaningful insights from such data becomes a daunting task. This is where dimensionality reduction techniques come into play, offering a powerful means of simplifying data without sacrificing crucial information. Among these techniques, Uniform Manifold Approximation and Projection (UMAP) has emerged as a leading contender, renowned for its ability to preserve both local and global structure in data.

Understanding UMAP: A Framework for Data Exploration

UMAP is a non-linear dimensionality reduction algorithm that leverages topological data analysis to create a low-dimensional representation of high-dimensional data. Its core principle lies in the assumption that data points residing in a high-dimensional space often lie on a lower-dimensional manifold. This manifold represents the underlying structure of the data, capturing the intrinsic relationships between data points. UMAP aims to uncover this manifold and project the data onto a lower-dimensional space while preserving the topological relationships between points.

The Key Components of UMAP

UMAP’s effectiveness stems from its unique combination of key components:

  • Neighborhood Graph Construction: UMAP begins by constructing a neighborhood graph that captures the local relationships between data points. This graph represents the interconnectedness of points based on their proximity in the high-dimensional space.
  • Manifold Approximation: The algorithm then seeks to approximate the underlying manifold of the data. This involves identifying the low-dimensional representation that best preserves the structure of the neighborhood graph.
  • Projection: Finally, UMAP projects the data points onto the lower-dimensional space, preserving the topological relationships captured in the manifold approximation.

Advantages of UMAP in Data Analysis

UMAP offers a range of advantages over other dimensionality reduction techniques, making it a powerful tool for data exploration and analysis:

  • Preservation of Global and Local Structure: UMAP excels at preserving both the global and local structure of data. This ensures that the low-dimensional representation accurately reflects the underlying relationships within the dataset.
  • Scalability and Efficiency: UMAP is designed to handle large datasets efficiently, making it suitable for real-world applications.
  • Intuitive Visualization: The low-dimensional representations generated by UMAP are often highly intuitive and visually appealing, enabling researchers to quickly grasp the underlying patterns in the data.
  • Robustness to Noise: UMAP is relatively robust to noise and outliers, making it reliable for analyzing real-world datasets.

Applications of UMAP in Diverse Fields

The versatility of UMAP has led to its widespread adoption across various domains, including:

  • Machine Learning: UMAP facilitates efficient feature extraction and dimensionality reduction in machine learning models, enhancing performance and interpretability.
  • Bioinformatics: UMAP is employed for visualizing and analyzing high-dimensional biological data, revealing hidden patterns in genomic, proteomic, and transcriptomic datasets.
  • Image Analysis: UMAP aids in reducing the dimensionality of image data, enabling efficient processing and analysis of large image collections.
  • Social Sciences: UMAP assists in understanding complex social networks, identifying clusters of individuals with shared characteristics and uncovering hidden relationships.

Frequently Asked Questions

Q1: What are the limitations of UMAP?

A1: While UMAP offers significant advantages, it’s important to note that it is not without limitations. One challenge lies in its sensitivity to the choice of parameters, such as the number of neighbors and the minimum distance. Careful parameter tuning is crucial for obtaining optimal results. Additionally, UMAP may struggle with datasets exhibiting highly complex or non-manifold structures.

Q2: How does UMAP compare to other dimensionality reduction techniques like t-SNE?

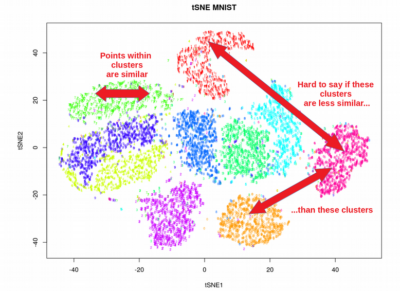
A2: UMAP and t-SNE are both non-linear dimensionality reduction algorithms, but they differ in their underlying principles and strengths. t-SNE excels at preserving local structure but may struggle with global relationships. UMAP, on the other hand, prioritizes preserving both local and global structure, making it more suitable for datasets with complex relationships.

Q3: Can UMAP be used for data visualization?

A3: Yes, UMAP is a powerful tool for data visualization. The low-dimensional representations generated by UMAP can be easily visualized using scatter plots, enabling researchers to gain insights into the underlying structure of the data.

Tips for Effective UMAP Implementation

  • Parameter Tuning: Experiment with different parameter settings to optimize the performance of UMAP for your specific dataset.
  • Data Preprocessing: Preprocessing data, such as scaling or standardizing features, can enhance the performance of UMAP.
  • Visual Interpretation: Analyze the generated low-dimensional representations carefully, considering the context of the data and the chosen parameters.
  • Combining with Other Techniques: UMAP can be effectively combined with other dimensionality reduction techniques or visualization methods to gain further insights.

Conclusion

UMAP has emerged as a powerful and versatile dimensionality reduction technique, offering a unique combination of advantages. Its ability to preserve both local and global structure, coupled with its scalability and efficiency, makes it an invaluable tool for exploring and analyzing complex high-dimensional datasets. As data science continues to advance, UMAP is poised to play a pivotal role in unlocking the hidden patterns and insights within increasingly complex data landscapes.

“Understanding UMAP’s Dimension Reduction Techniques: Key Concepts Explained” – AI News Dimensionality reduction: Uniform Manifold Approximation and Projection (UMAP) - YouTube UMAP Dimensionality Reduction - An Incredibly Robust Machine Learning Algorithm by Saul
UMAP: An alternative dimensionality reduction technique by Fernando Luna MCD-UNISON Medium UMAP method- Dimensionality Reduction in Single Cell Genomics - Dolomite Bio PCA and UMAP dimensionality reduction of GTEx and Pan-Cancer Atlas Download Scientific Diagram
Dimensionality Reduction : PCA, tSNE, UMAP - Auriga IT UMAP dimensionality reduction of Z for the EyePACS dataset. The top row Download Scientific

Closure

Thus, we hope this article has provided valuable insights into Unveiling the Power of Dimensionality Reduction: A Comprehensive Look at UMAP. We thank you for taking the time to read this article. See you in our next article!